#2042: Rolle's Theorem explain

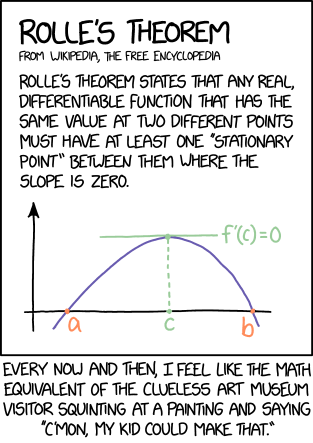
[A single framed picture shows a colored x-y-graph with a text above:]

Rolle’s Theorem

From Wikipedia, the free encyclopedia

Rolle’s theorem states that any real, differentiable function that has the same value at two different points must have at least one “stationary point” between them where the slope is zero.

[The graph shows a sine like curve in blue intersecting the x-axis at points “a” and “b” marked in red while in the middle a point “c” has a vertical dashed green line to the apex and on top also in green f’(c)=0 is drawn with a horizontal tangent line.]

[Caption below the frame:]

Every now and then, I feel like the math equivalent of the clueless art museum visitor squinting at a painting and saying “c’mon, my kid could make that.”