#2048: Curve-Fitting explain

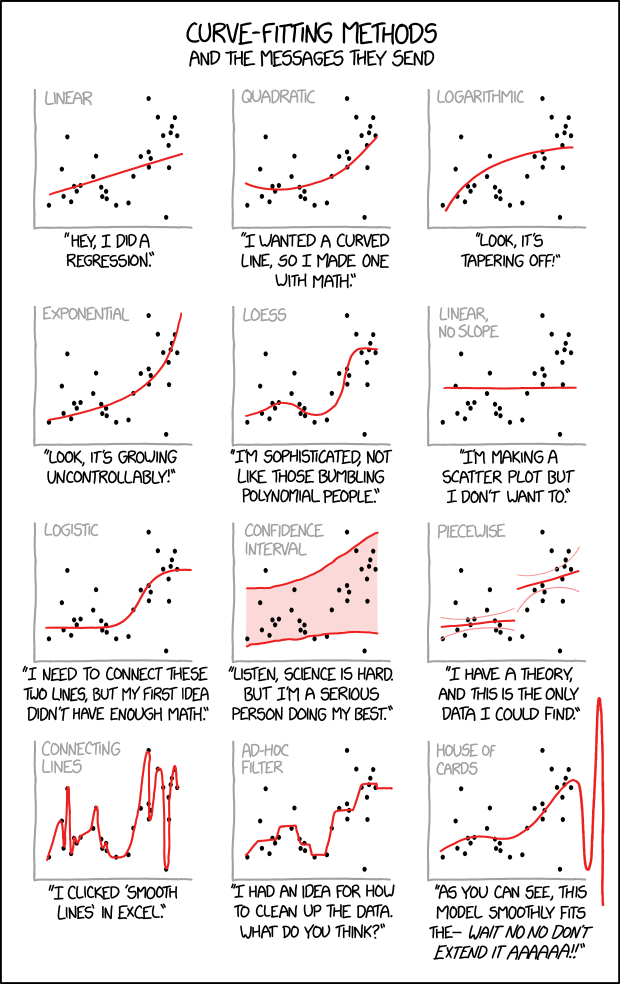
Curve-Fitting Methods

and the messages they send

[In a single frame twelve scatter plots with unlabeled x- and y-axes are shown. Each plot consists of the same data-set of approximately thirty points located all over the plot but slightly more distributed around the diagonal. Every plot shows in red a different fitting method which is labeled on top in gray.]

[The first plot shows a line starting at the left bottom above the x-axis rising towards the points to the right.]

Linear

“Hey, I did a regression.”

[The second plot shows a curve falling slightly down and then rising up to the right.]

Quadratic

“I wanted a curved line, so I made one with math.”

[At the third plot the curve starts near the left bottom and increases more and more less to the right.]

Logarithmic

“Look, it’s tapering off!”

[The fourth plot shows a curve starting near the left bottom and increases more and more steeper towards the right.]

Exponential

“Look, it’s growing uncontrollably!”

[The fifth plot uses a fitting to match many points. It starts at the left bottom, increases, then decreases, then rapidly increasing again, and finally reaching a plateau.]

LOESS

“I’m sophisticated, not like those bumbling polynomial people.”

[The sixth plot simply shows a line above but parallel to the x-axis.]

Linear, no slope

“I’m making a scatter plot but I don’t want to.”

[At plot #7 starts at a plateau above the x-axis, then increases, and finally reaches a higher plateau.]

Logistic

“I need to connect these two lines, but my first idea didn’t have enough Math.”

[Plot #8 shows two red lines embedding most points and the area between is painted as a red shadow.]

Confidence interval

“Listen, science is hard. But I’m a serious person doing my best.”

[Plot #9 shows two not connected lines, one at the lower left half, and one higher at the right. Both have smaller curved lines in light red above and below.]

Piecewise

“I have a theory, and this is the only data I could find.”

[The plot at the left bottom shows a line connecting all points from left to right, resulting in a curve going many times up and down.]

Connecting lines

“I clicked ‘Smooth Lines’ in Excel.”

[The next to last plot shows a echelon form, connecting a few real and some imaginary points.]

Ad-Hoc filter

“I had an idea for how to clean up the data. What do you think?”

[The last plot shows a wave with increasing peak values. Finally the plot of the wave is continued beyond the x- and y-axis borders.]

House of Cards

“As you can see, this model smoothly fits the- wait no no don’t extend it AAAAAA!!”